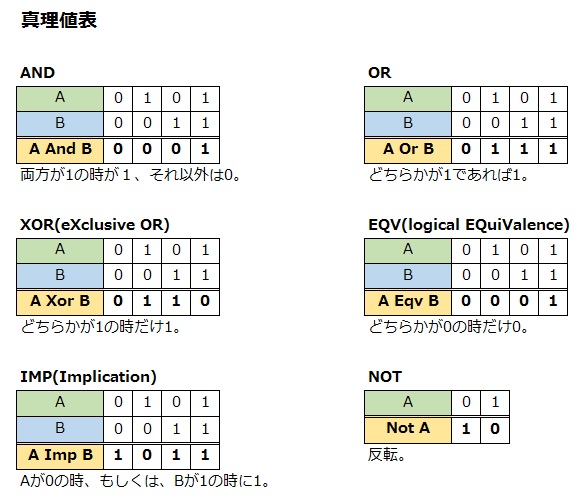
真理値表または真理値表は、論理的推論の分野で広く使用されている数学ツールです。その目的は、複合命題 (2 つ以上の単純な命題によって形成される議論) の論理的妥当性を検証することです。
複合命題の例:
- ジョンは背が高く、メアリーは背が低い。
- ペドロは背が高い、またはジョアナは金髪です。
- ペドロが背が高いなら、ジョアナは赤毛です。
上記の複合命題はそれぞれ、太字の接続詞で結合された 2 つの単純な命題によって形成されます。それぞれの単純な命題は真か偽の可能性があり、これは複合命題の論理値を直接暗示します。 「ジョンは背が高く、メアリーは背が低い」という表現を採用すると、このステートメントの考えられる評価は次のようになります。
- ジョンが背が高く、メアリーが背が低い場合、「ジョンは背が高く、メアリーは背が低い」という文は TRUE になります。
- ジョンが背が高く、メアリーが背が低くない場合、「ジョンは背が高く、メアリーは背が低い」という文は FALSE になります。
- ジョンが背が高くなく、メアリーが背が低い場合、「ジョンは背が高く、メアリーは背が低い」という文は FALSE になります。
- ジョンが背が高くなく、メアリーが背が低くない場合、「ジョンは背が高く、メアリーは背が低い」という文は FALSE になります。
真理値表は、これと同じ推論 (以下の結合トピックを参照) をより直接的な方法で概説しています。さらに、真理値表の規則は、文中の命題の数に関係なく適用できます。
どのように機能するのでしょうか?
まず、質問の命題を論理で使用される記号に変換します。広く使用されている記号のリストは次のとおりです。
| シンボル | 論理演算 | 意味 | 例 |
|---|---|---|---|
| p | 。 | 提案 1 | p = ジョアンは背が高い。 |
| q | 。 | 提案 2 | q = マリアは背が低いです。 |
| ~ | 拒否 | いいえ | ジョアンが背が高い場合、「 ~p 」は FALSE になります。 |
| ^ | 接続詞 | そして | p ^ q = ジョンは背が高く、メアリーは背が低い。 |
| v | 論理和 | または | p v q = ジョンは背が高い、またはメアリーは背が低い。 |
| → | 条件付き | もし…それなら | p → q = ジョンが背が高いなら、メアリーは背が低い。 |
| ↔ | 二条件付き | もし、そしてその場合に限り | p ↔ q = メアリーが背が低い場合に限り、ジョンは背が高くなります。 |
次に、複合命題を評価するためのすべての可能性を記載した表が作成され、ステートメントが記号に置き換えられます。 3 つ以上の命題がある場合、それらはr 、 sなどの文字で記号化できることを明確にしておきます。
最後に、示されている接続詞によって定義された論理演算が適用されます。上記のリストによると、これらの演算には、否定、論理積、論理和、条件付き、および双条件付きがあります。
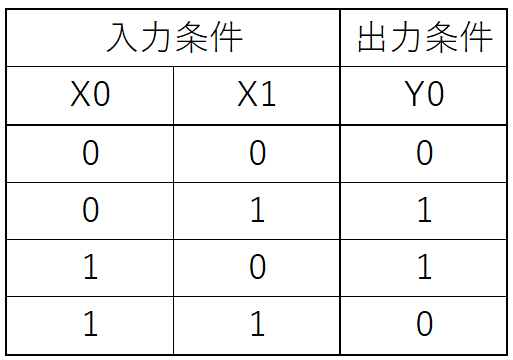
拒否
否定は~ で表されます。否定の論理演算は最も単純であり、多くの場合、真理値表を使用する必要はありません。同じ例に従うと、ジョアンは背が高い (p) 場合、ジョアンは背が高くない (~p) と言うのは FALSE であり、その逆も同様です。

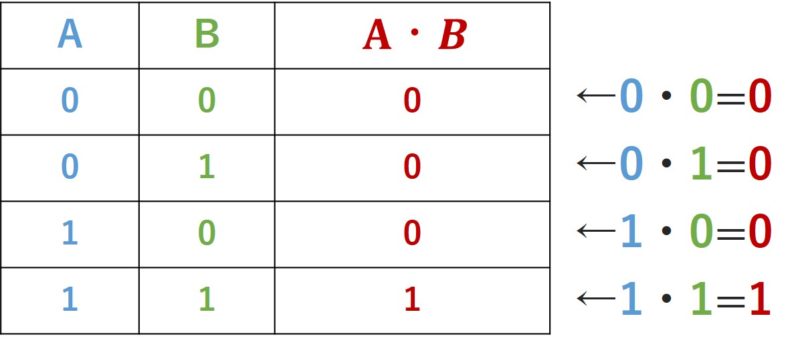
接続詞
接続詞は^で表されます。 「ジョンは背が高く、メアリーは背が低い」の例は「p ^ q」で記号化され、真理値表は次のようになります。
接続詞は累積の概念を示唆しているため、単純な命題の 1 つが偽である場合、複合命題が真であることは不可能です。
結論: 接続複合命題 (接続詞と を含む) は、その要素がすべて true の場合にのみ true になります。
例:
「パウロ、レナト、トゥーリオは親切で、カロリーナは面白いです。」
– パウロ、レナト、トゥーリオが親切でないか、カロリーナが面白くない場合、この命題は偽になります。複合命題が真であるためには、すべての情報が真でなければなりません。

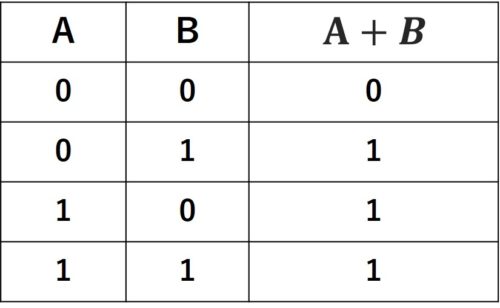
論理和
論理和はvで表されます。上の例の接続詞をorに変更すると、「ジョンは背が高い、またはメアリーは背が低い」になります。この場合、文は「p v q」で記号化され、真理値表は次のようになります。
論理和は交互のアイデアを意味するため、単純な命題の 1 つが真であれば、複合体も同様に真であれば十分です。
結論: 選言的複合命題 (接続詞または を含む) は、そのすべての要素が false の場合にのみ false になります。
例:
「お母さん、お父さん、または叔父さんが私にプレゼントをくれるでしょう。」
– この発言が真実であるためには、母親、父親、または叔父のいずれか 1 人だけが贈り物をするだけで十分です。命題は、誰もそれを与えない場合にのみ偽になります。
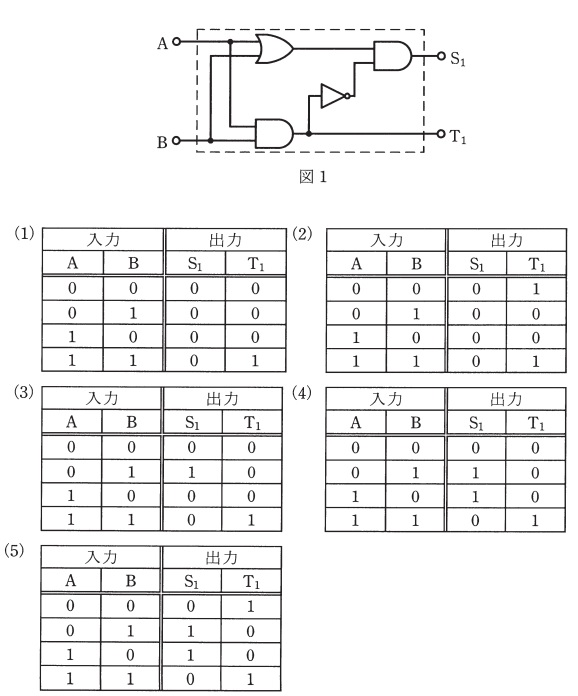
条件付き
条件文は→で表されます。それは、単純な命題を因果関係で相互接続する接続詞ifとthenによって表現されます。 「パウロがリオ出身なら、彼はブラジル人です」の例は「p → q」となり、真理値表は次のようになります。
条件文には、接続詞thenで区切られた先行詞と後件命題があります。条件文を分析するときは、前件と後件の含意関係を考慮して、どのような場合に命題が可能であるかを評価する必要があります。
結論: 条件付き複合命題 (接続詞ifとthenを含む) は、最初の命題が true で 2 番目の命題が false の場合にのみ false になります。
例:
「もしパウロがリオ出身なら、彼はブラジル人だ。」
– この命題が TRUE であるとみなされるためには、それが可能であるケースを評価する必要があります。上記の真理値表によれば、次のようになります。
1. パウロはリオ出身 / パウロはブラジル人 = 可能性があります
2. パウロはリオ出身 / パウロはブラジル人ではない =不可能
3. パウロはリオ出身ではありません / パウロはブラジル人です = 可能性があります
4. パウロはリオ出身ではありません / パウロはブラジル人ではありません = 可能性があります
二条件付き
二条件は↔で表されます。これは、単純な命題を同値関係で相互接続する接続詞ifとif のみを介して読み取られます。 「ジョンはメアリーが微笑むときだけ幸せです。」の例。は「p ↔ q」となり、真理値表は次のようになります。
二条件は相互依存の考え方を示唆しています。名前自体が示すように、双条件は 2 つの条件で構成されます。1 つはpからqに向かう (p → q)、もう 1 つは逆方向 (q → p) です。
結論: 二条件複合命題 ( ifとif のみの接続詞を含む) は、すべての命題が真であるか、すべての命題が偽である場合にのみ真になります。
例:
「ジョンはメアリーが微笑むときだけ幸せです。」
–これは次のことを意味します:
1. ジョンが幸せならメアリーは微笑み、メアリーが微笑めばジョンは幸せになる = TRUE
2. ジョンが幸せでない場合、メアリーは笑わない、メアリーが笑わない場合、ジョンは幸せではない = TRUE
3. ジョンが幸せなら、メアリーは笑わない = FALSE
4. ジョンが幸せでないとメアリーは微笑む = FALSE

概要
真理値表の研究者は、各論理演算の結論を暗記するのが一般的です。問題解決の時間を節約するには、次のことに常に留意してください。
- 接続命題:すべての要素が true の場合にのみ true になります。
- 選言命題:すべての要素が偽の場合にのみ偽となります。
- 条件付き命題:最初の命題が真で 2 番目の命題が偽の場合にのみ偽となります。
- 二条件命題:すべての要素が true であるか、すべての要素が false である場合にのみ true になります。
参考画像一覧




参考動画一覧
論理演算・真理値表・回路AND・OR・NOT【高校情報授業・ITパスポート・基本情報技術者】
【電験3種】論理回路と真理値表と論理式(デジタル回路)
論理演算の基本.v1/ITパスポート・基本情報技術者・高校情報
【経済数学(ガチ)】Retake版-01. 02:論理積・論理和・論理否定,真理値表,ド・モルガンの法則とその一般化【命題論理の基礎編】