フィボナッチ数列

フィボナッチ数列は、後続の各要素が前の 2 つの要素の合計で あるパターンに従う無限の連続する数値 で構成されます。したがって、0 と 1 の後には、1、2、3、5、8、13、21、34、55、89、144 などが続きます。

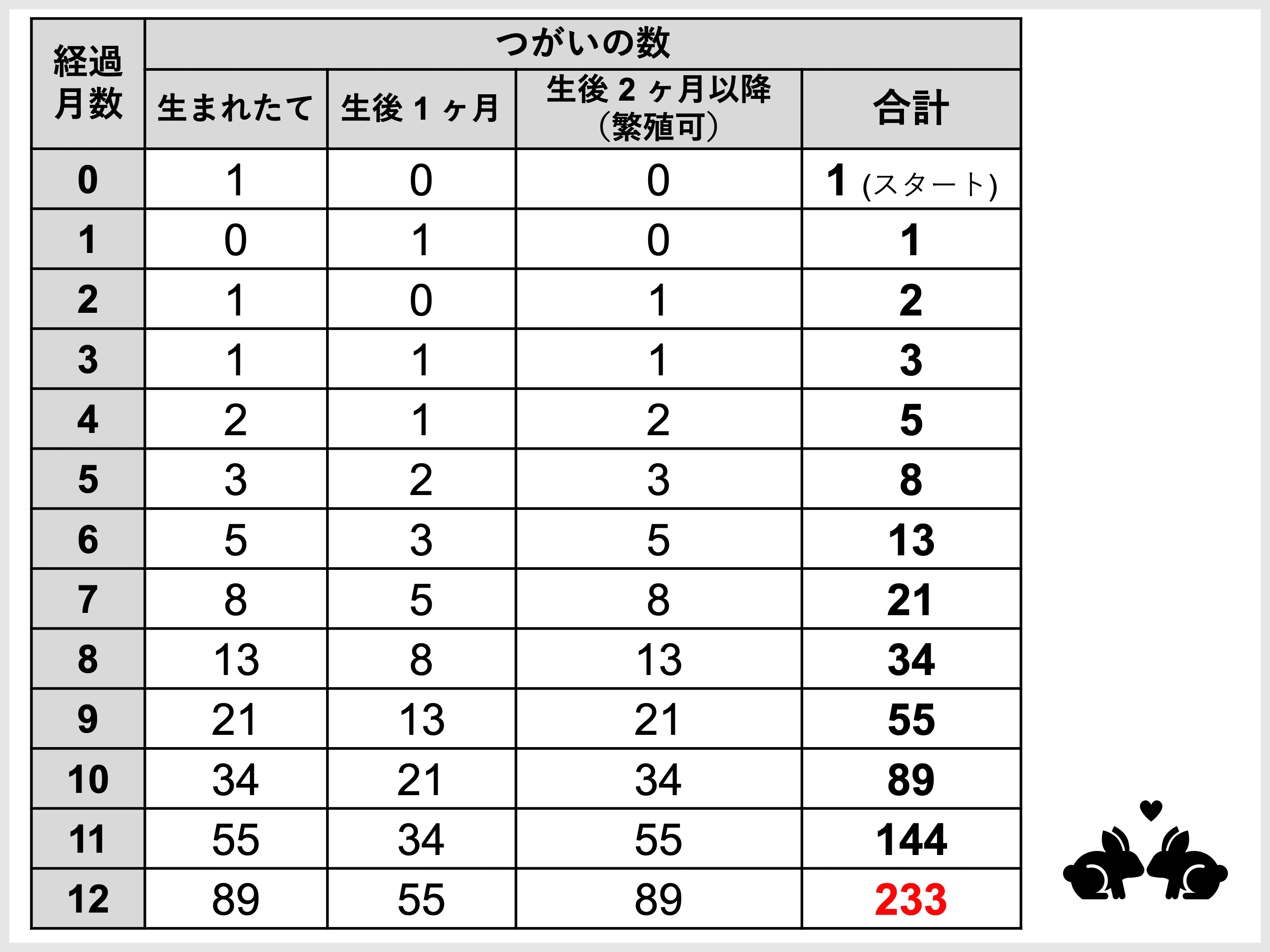
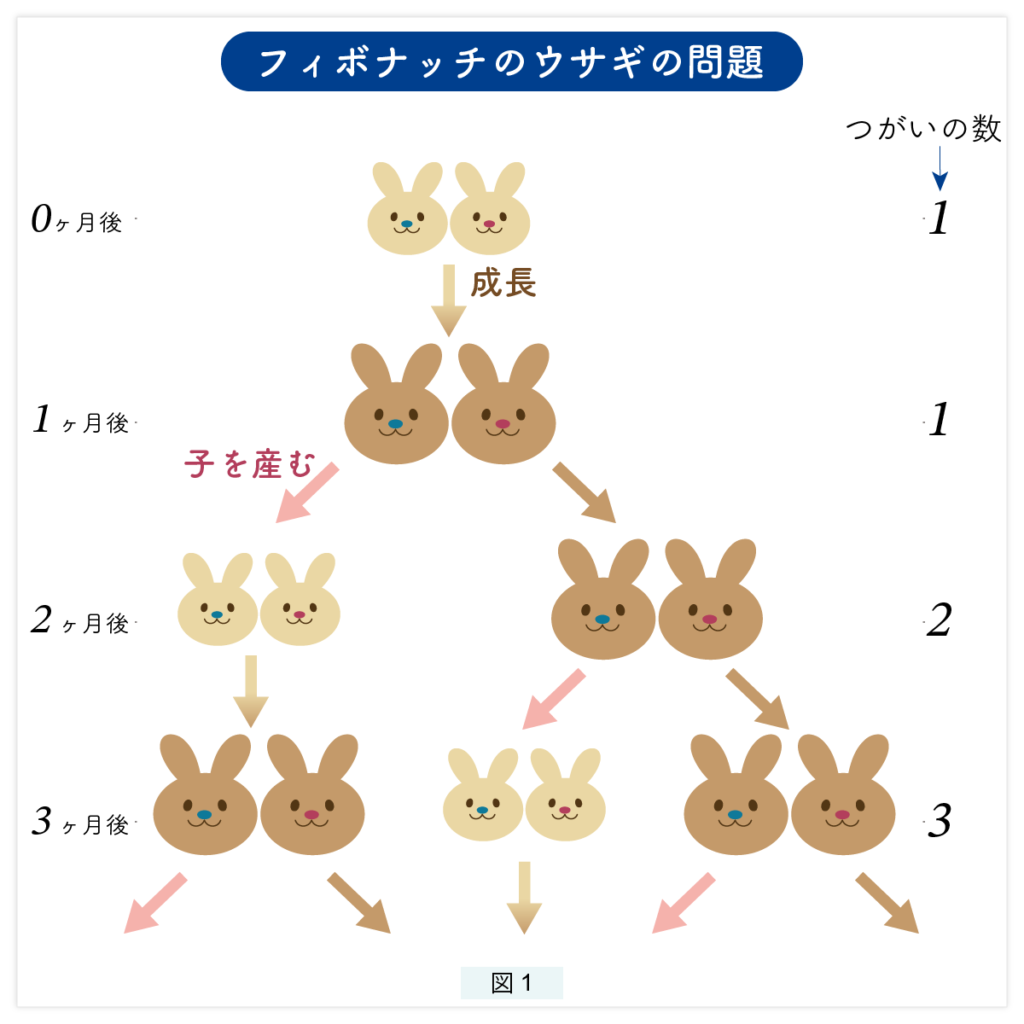
この数列は、レオナルド ピサまたはレオナルド ビゴッロとしても知られるイタリアの数学者 レオナルド フィボナッチ (1170 – 1250) によって発見されました。フィボナッチの観察は、ウサギの集団の成長を観察することによって行われました。

シーケンスは数字の 0 と 1 で始まり、これが繰り返され、最後の 2 つの数字の合計が次の数字を形成します: 1 + 1 = 2。その後、シーケンスは加算され続けます: 1 + 2 = 3。 2 + 3 = 5; 3 + 5 = 8;など無限に続きます。

長年にわたる数学研究が示しているように、この一連の数字は不思議なことに、さまざまな自然現象と相互に関連しています。

フィボナッチ数列の数値は、いわゆる 「黄金比率」 を形成します。これは、人間の目に心地よいと考えられているため、美術、建築、デザインに広く適用されている視覚的な概念です。黄金比の値は約 1.6 で、フィボナッチ数列で数値を前の数値で割ったときに得られるのはまさにこの数値です。

黄金比 について詳しくはこちらをご覧ください。

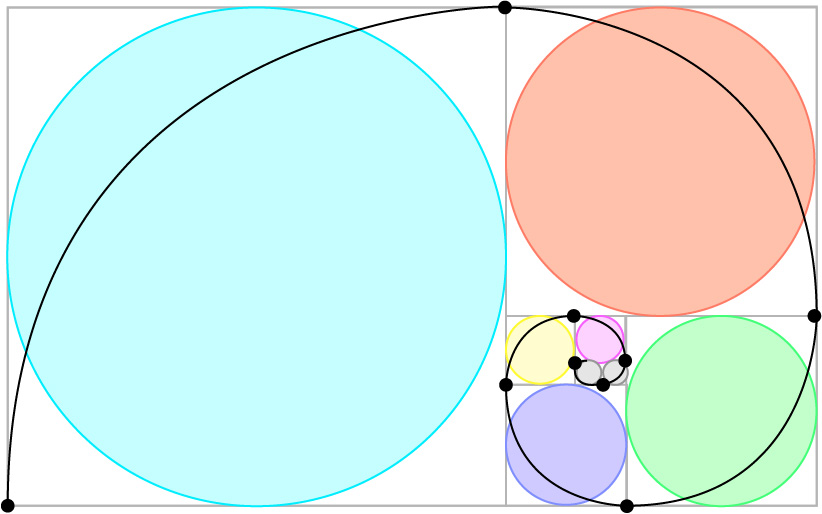
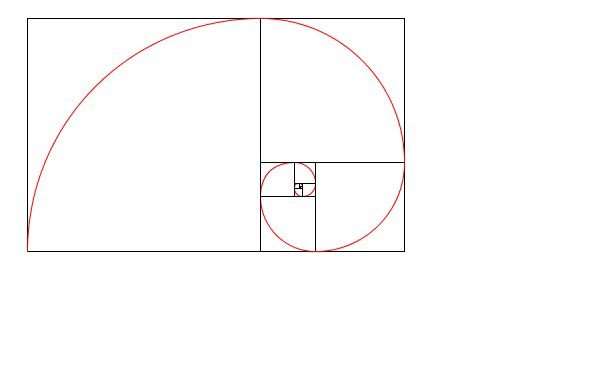
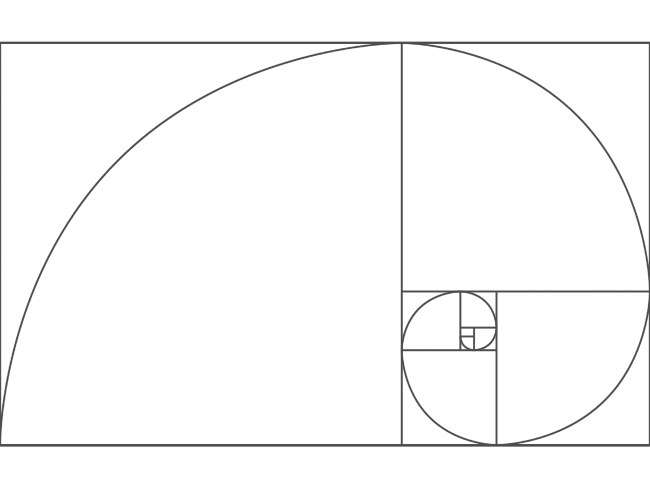
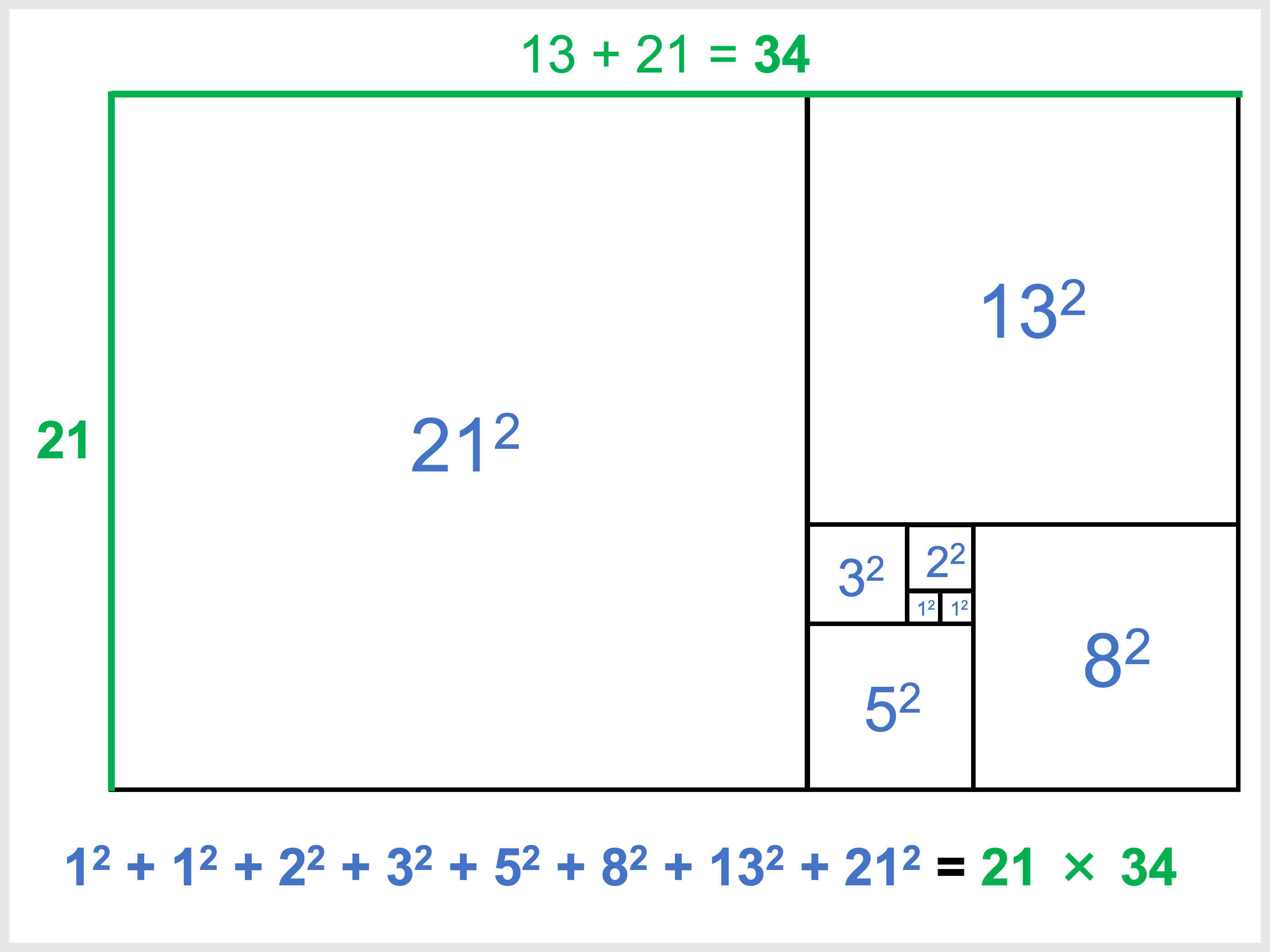
このシーケンスから、 黄金長方形 のアイデアを構築することができます。長方形内で分割された各正方形の内側に円弧を描くと、フィボナッチスパイラルも観察されます。

このシーケンスの観察から得られた黄金比のアイデアは、たとえばレオナルド・ダ・ヴィンチによって人体の完璧な姿を説明するために使用されました。

「ウィトルウィウス的人体図 」も参照してください。