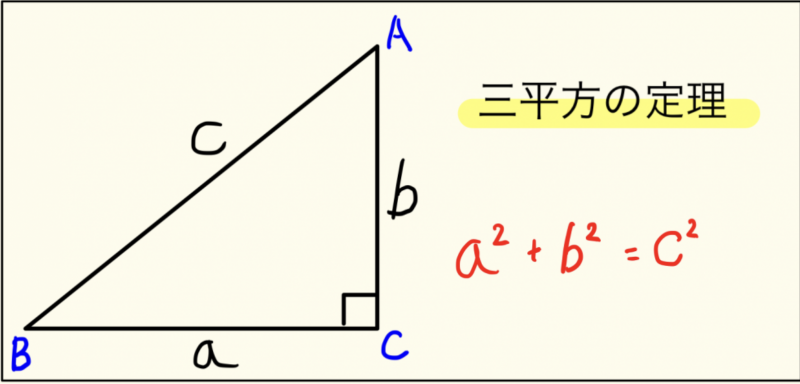
ピタゴラスの定理は、直角三角形の辺の長さの関係を記述する 数学幾何学の原理 です。
原理は「 斜辺の二乗は脚の二乗の和に等しい 」というものです。斜辺と脚は三角形の辺に付けられた名前です。
ピタゴラスの定理は直角三角形でのみ使用できます。 直角三角形とは 、直角、つまり90度の角度を持つ三角形のことです。
ピタゴラスの定理の公式を理解してください。
a 2 + b 2 = c 2
式では、A と B は三角形の脚、C は斜辺です。
ピタゴラスの定理の計算方法
ピタゴラスの定理は、直角三角形の他の 2 つの辺がわかっている場合に、1 つの辺の値を求めるために使用されます。この式は、2 本の脚の値を 2 乗すると、斜辺の値の 2 乗が得られることを示しています。
式 a 2 +b 2 =c 2 (a と b は脚、c は斜辺) を使用すると、未知の値を見つけることができます。 a = 4 および b = 3 と仮定します。c の値はどうなるでしょうか?計算がどのように行われるかを理解します。
式では、a と b の既知の値がそれぞれ 4 と 3 に置き換えられます。次に、これらの数値を 2 乗し、その数値を掛け合わせます (4×4=16 および 3×3=9)。次に、見つかった値 16 と 9 を加算すると、結果は 25 になります。
この値 25 は C の 2 乗に等しく、C の実際の値を見つけるには、25 の平方根、つまり 5 を求める必要があります。したがって、C は 5 に等しいです。要約すると、この小さな問題では次のようになります。辺 a = 4、辺 b = 3、斜辺 = 5。
斜辺と脚
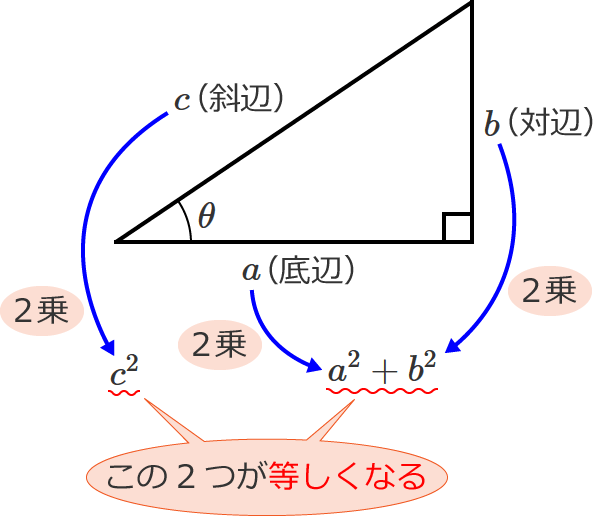
脚は 、内直角である 90 度の角度を構成する三角形の辺であることを覚えておく価値があります。 斜辺は 90度の角度の反対側の辺であり、直角三角形の最も長い辺です。
三角形の種類 についても学びましょう。

ピタゴラスの定理の使用例
ピタゴラスの定理をより深く理解するには、他の例を参照してください。

脚の 1 つを見つけるための演習
-
直角三角形の斜辺の長さは 10 cm、一方の脚の長さは 6 cm です。もう一方の脚の長さはいくらですか。
答え : 反対側は8cmです。 -
直角三角形の斜辺は 15 で、片方の脚は 9 ですが、2 番目の脚の長さはいくらですか?
回答 : 2 番目の脚の長さは 12 です。
完全な九九 も参照してください。

斜辺を見つける練習
-
ピタゴラスの定理の公式では、a と b は脚を表し、c は斜辺を表します。直角三角形は a = 5、b = 12 になります。c の長さはいくらですか?
答え : c の長さは 13 です。 -
土地は直角三角形の形をしています。農家は、土地を囲うのに必要な資材の量を決定するために、斜辺の長さを計算する必要があります。彼は脚を測定したところ、a = 7 メートル、b = 24 メートルであることがわかりました。斜辺の長さはどれくらいですか?
回答 : 地形の斜辺は 25 メートルです。

ピタゴラスの定理の歴史
ピタゴラスの定理は、その作成者の名前にちなんで名付けられました。ピタゴラスは紀元前 569 年に 古代ギリシャの サモスで生まれ、ソクラテス以前の偉大な思想家であり、哲学と数学に影響を与えた ピタゴラス主義 の創始者でした。
貿易商の息子だったピタゴラスは、良い教育を受け、さまざまな地域を旅して、さまざまな民族や彼らの数学の使い方に触れる機会があっただろう。ピタゴラスはエジプトに住んでいたことが知られていますが、インドやアラビアに到達したとも考えられています。
成長すると、ピタゴラスは落ち着いて知識だけに専念し、世界は数字で構成されているという考えに基づいたピタゴラス学派を設立しました。彼には何百人もの学者や信者がいました。
この時期に彼はピタゴラスの定理を定式化したと考えられていますが、数学者によって書かれた文書はなく、彼の仕事について知られているのは口頭での伝達と彼の信者の記録の結果です。
参考画像一覧

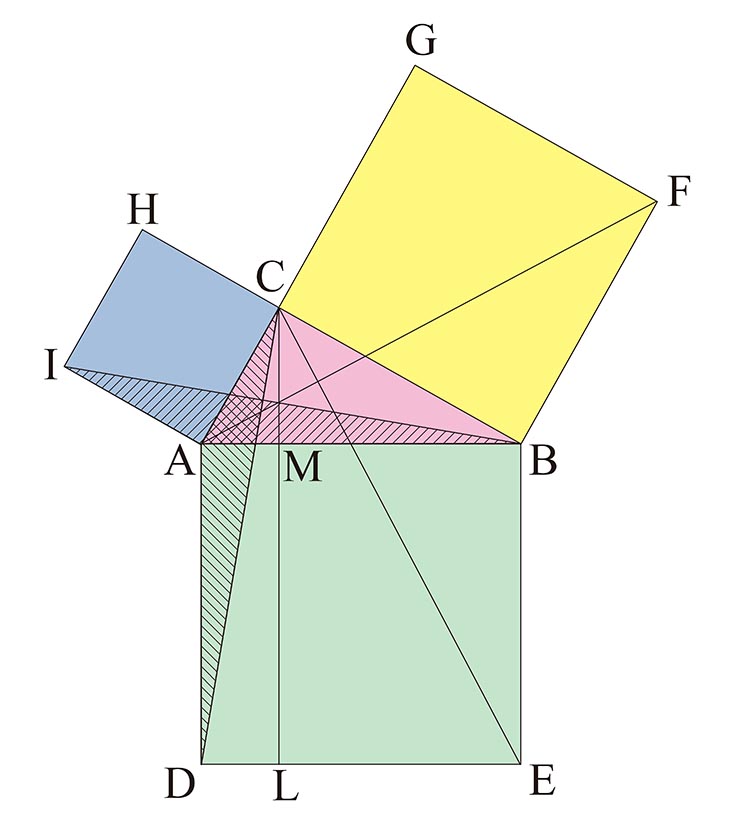
3.png)



.jpg)



参考動画一覧
「ピタゴラスの定理」の証明アニメ6(ユークリッド)
【ピタゴラスの定理】三平方の定理 証明10選 中3 中学 数学
【中3 数学】三平方の定理(ピタゴラスの定理)
【ピタゴラスの定理】視覚的に見て分かる三平方の定理の証明が面白い!【物理エンジン】